Christopher Bridges

Game Development Master’s student

Project Idea

The core idea for my project is to create a procedurally generated dungeon system using a Binary Space Partitioning (BSP) algorithm. This method divides the available space into smaller sections recursively, providing a structured and efficient way to generate unique dungeon layouts with each playthrough.

Using BSP, I aim to focus on the following key aspects:

  • Room Division: Dividing the dungeon space into regions that will serve as individual rooms or hallways.
  • Connectivity: Ensuring all rooms are logically connected with corridors to form a cohesive and navigable dungeon.
  • Scalability: Designing the system to handle various dungeon sizes and complexities by tweaking parameters like room size or recursion depth.

The modular nature of BSP will allow me to build a flexible and reusable dungeon generation system that can adapt to different use cases. Each component of the generation process will operate independently while seamlessly coming together in the final implementation.

This project will focus purely on the generation mechanics, aiming to strike a balance between randomness and logical structure to create layouts that are unique yet functional.

“Binary Space Partitioning is implemented for recursively subdividing a space into two convex sets by using hyperplanes as partitions. This process of subdividing gives rise to the representation of objects within the space in the form of tree data structure known as BSP Tree” (GeeksforGeeks 2020).

A BSP tree (GeeksforGeeks 2020)

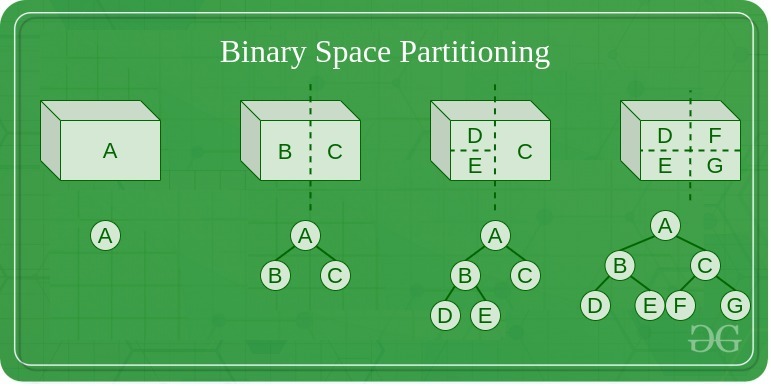
To implement a BSP algorithm for the procedural dungeon generation, there are some key steps that will need to be taken:

  • Define the size of the dungeon space and the constraints on the room size
  • Recursively split the initial area to produce rooms
  • After the BSP algorithm has partitioned the space into smaller areas, treat each resulting “leaf” node as a room
  • Connect each room with corridors
  • Generate walls around the rooms and corridors

Reference List

GeeksforGeeks. (2020). Binary Space Partitioning Martinez. [online]. Available from: https://www.geeksforgeeks.org/binary-space-partitioning/ [accessed 23 October].

Updated: